System of Linear Equations

- Indra B. Kshattry PhD

Definition:

A system of linear equations is a set of two or more linear equations involving the same variables. The solution to the system is the set of values for the variables that satisfy all equations simultaneously. Each equation in the system represents a line (or a hyperplane in higher dimensions), and the solution to the system is the point or set of points where these lines (or hyperplanes) intersect.

General form:
A linear equation in \(n\) variables \( x_1,x_2,…,x_n \) can be written as: $$ a_1 x_1 + a_2 x_2 + a_3 x_3 + ... + a_n x_n = b $$ where \( a_1, a_2, a_3, ... , a_n\) are real numbers called coefficients, and 𝑏 is a constant term.
A system of \(m\) linear equations in \(n\) variables is a set of equations of the form: $$ a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + ... + a_{1n}x_n = b_1 $$ $$ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 + ... + a_{2n}x_n = b_2 $$ $$ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 + ... + a_{3n}x_n = b_1 $$ $$ ... $$ $$ ... $$ $$ a_{m1}x_1 + a_{m2}x_2 + a_{m3}x_3 + ... + a_{mn}x_n = b_m $$ where,
\(a_{ij},   (1 \le i \le m;   1 \le j \le n)\)   are coefficients, \(x_j\),   \((1 \le j \le n)\) are variables, and \(b_i\), \((1 \le i \le m )\) are constant terms.

Two variables

General form:
A system of two linear equations in two variables 𝑥 and 𝑦 can be written as: $$ a_1x + b_1y = c_1 $$ $$ a_2x + b_2y = c_2 $$ where \(a_1, b_1, c_1, a_2, b_2, c_2\) are constants, and \(x\), \(y\) are the unknowns.

Example:
$$ 2x + 3y = 5 $$ $$ 4x - y = 3 $$

Three variables

General form:
A system can also be extended to three variables: $$ a_1x + b_1y + c_1z = d_1 $$ $$ a_2x + b_2y + c_2z = d_2 $$ $$ a_3x + b_3y + c_3z = d_3 $$ where 𝑥, 𝑦, 𝑧 are unknowns, and the coefficients are real numbers.

Example:
$$ x + 2y + z = 6 $$ $$ 2x - y + 3z = 14 $$ $$ -x + y - 2z = -2 $$

Methods of Solving a System of Linear Equations

There are several methods to solve a system:

1. Substitution Method
   • Solve one equation for one variable in terms of the other.
   • Substitute this expression into the second equation and solve.
2. Elimination (Addition) Method
   • Multiply equations if necessary to align coefficients.
   • Add or subtract equations to eliminate one variable.
   • Solve for the remaining variable.
3. Matrix Method (Gaussian Elimination)
   • Convert the system into an augmented matrix.
   • Use row operations to achieve row-echelon form.
   • Solve using back-substitution.
4. Cramer’s Rule (For square systems with a unique solution)
   • Uses determinants to find solutions.
5. Graphical Method
   • Plot each equation as a line on a graph.
   • The intersection point gives the solution.

Types of solution

A system of linear equations can have:

1. A Unique Solution (Consistent and Independent System)
   • The equations represent two distinct lines that intersect at a single point.
   • Example: $$ x + y = 2 $$ $$ 2x - y = 1 $$ Solving, we find 𝑥 = 1, 𝑦 = 1 so the solution is (1, 1).
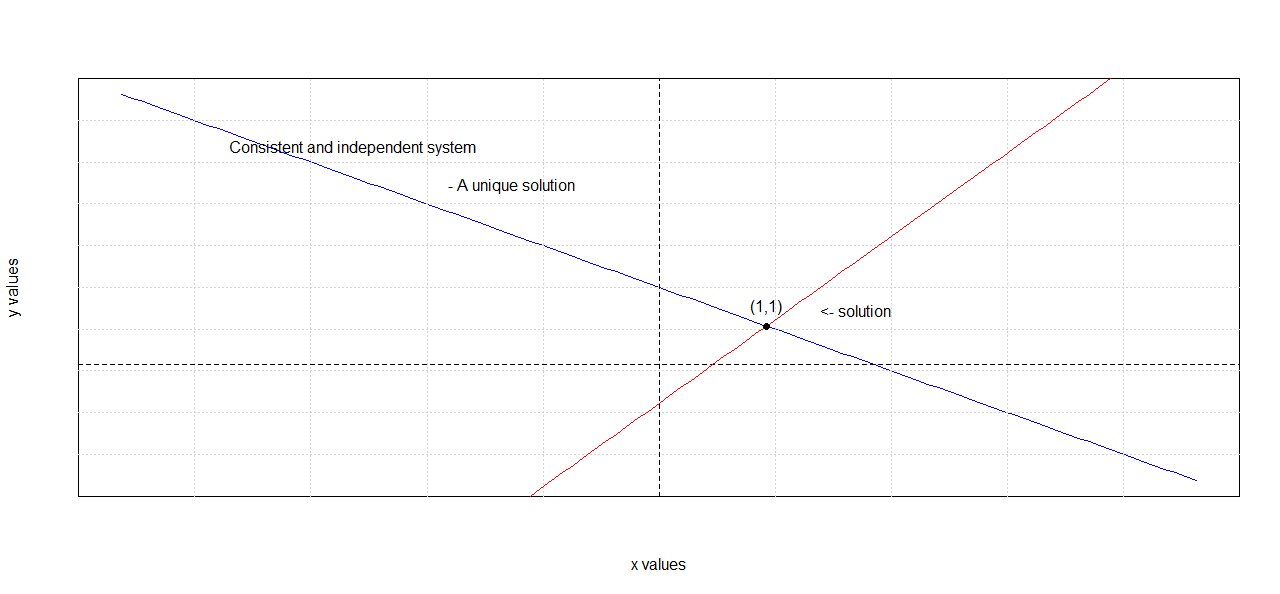
2. No Solution (Inconsistent System)
   • The equations represent parallel lines that never intersect.
   • Example: $$ 2x + y = 5 $$ $$ 4x + 2y = 12 $$ If we multiply the first equation by 2, we get \(4x + 2y = 10\), which contradicts \(4x + 2y = 12 \)
     Thus, no solution exists.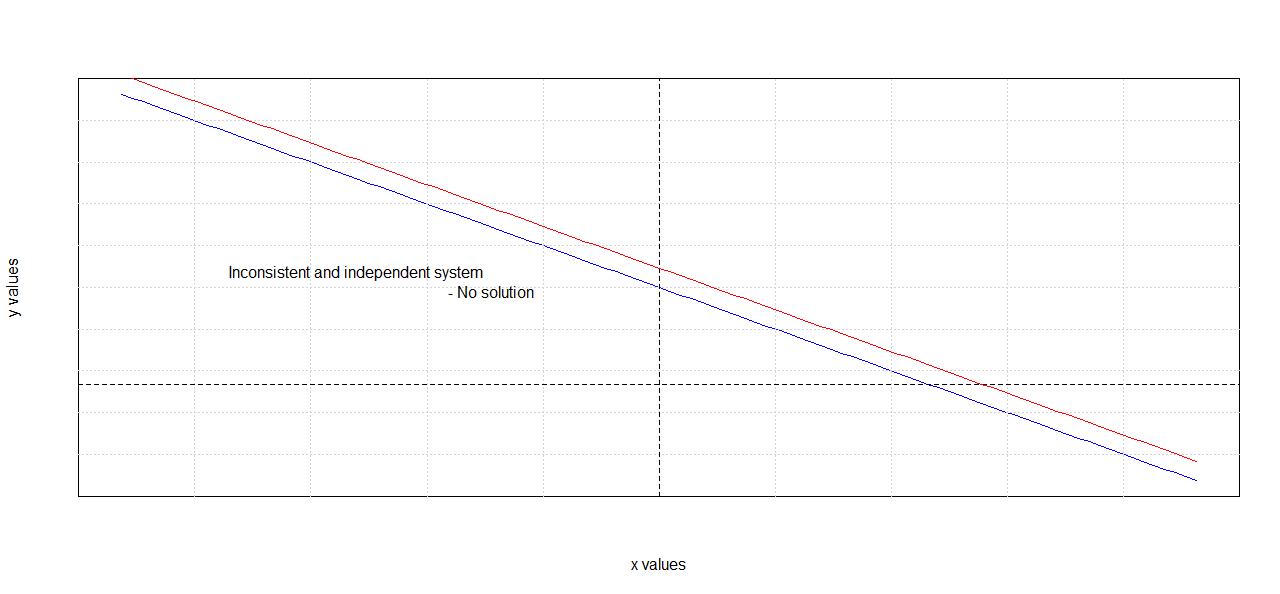
3. Infinitely Many Solutions (Consistent and Dependent System)
   • The equations represent the same line, meaning every point on the line is a solution.
   • Example:
     $$ 2x + y = 5 $$ $$ 4x + 2y = 10 $$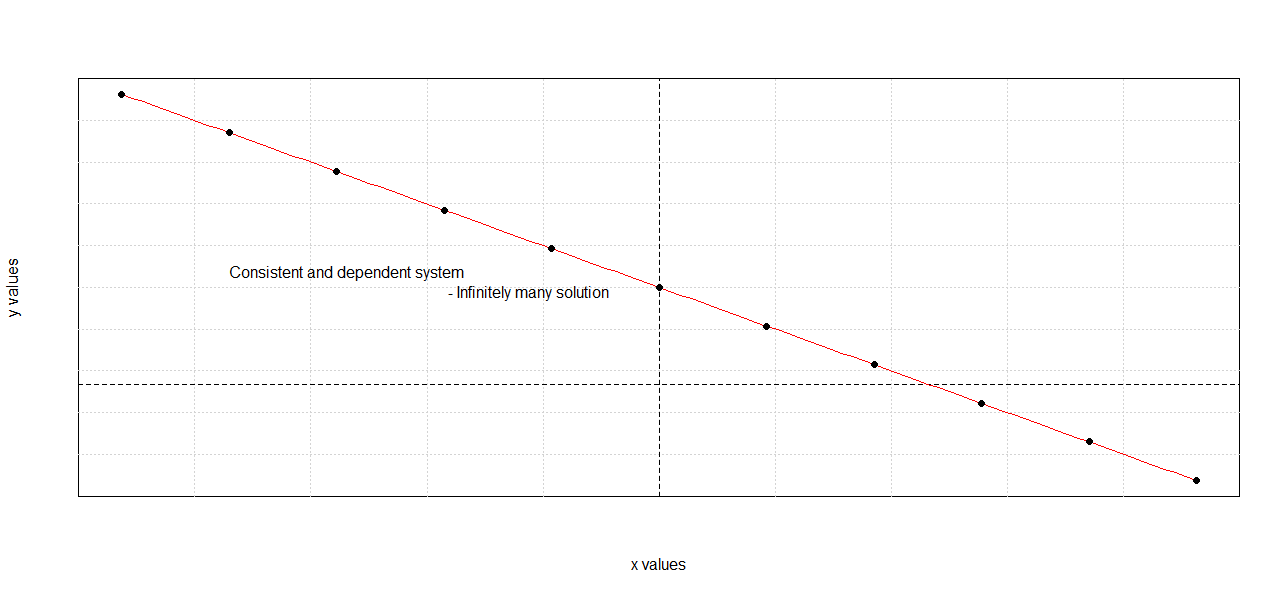
     Dividing the second equation by 2 gives \(2x + y = 5 \), which is the same as the first equation.

© Author: 2025